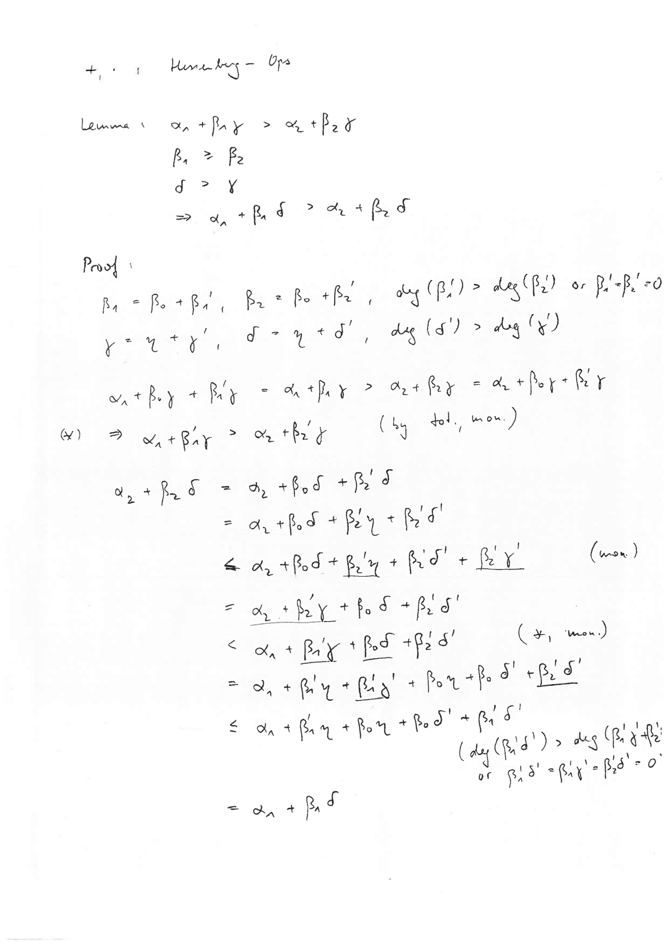November 2016
- From the AAR President, Larry Wos
- Results of CADE Trustee Elections
- Christoph Weidenbach follows Maria Paola Bonacina as President of CADE
- Search for New AAR Newsletter Editor
- Helmut Veith Stipend
- The TPTP Needs Money
- Winter Schools
- Special Issue
- Conferences
- MEMCODE 2016: Methods and Models for System Design, Call for Participation
- AITP 2017: Artificial Intelligence and Theorem Proving
- SCSS 2017: Symbolic Computation in Software Science
- LICS 2017: Logic in Computer Science
- CAV 2017: Computer-Aided Verification
- CADE-26: Conference on Automated Deduction
- CSL 2017: Computer Science Logics
- iFM 2017: Integrated Formal Methods, Call for Workshops
- FroCoS 2017: Frontiers of Combining Systems
- ITP 2017: Interactive Theorem Proving
- TABLEAUX 2017: Analytic Tableaux and Related Methods
- TABLEAUX / FroCoS / ITP 2017, Call for Workshops and Tutorials
- Workshops
- Book
- Open Positions
- Galois is Hiring in Oregon and Virginia, USA
- Several Positions on Secure Compilation at Inria Paris, France
- Several Positions on Higher-Order Proof Automation at VU Amsterdam, the Netherlands, and Inria Nancy, France
- Postdoc Position in Verification of Infinite-State Systems at the University of Iowa, USA
- Postdoc Position in Interactive Theorem Proving at Inria Sophia Antipolis, France
- Ph.D. Position in Formal Methods for Information Security at ETH Zürich, Switzerland
- Research Internships in Program Analysis at Google in California and New York, USA
- Opportunities in SAT and SMT and Related Areas
- Counting of the Ballots of the CADE Trustee Elections
- The Editor's Corner
From the AAR President, Larry Wos
When I introduce automated reasoning to a new researcher, a mathematician, a logician, or some other scientist, I emphasize the importance of strategy. I discuss strategy to restrict reasoning, strategy to direct reasoning, and other types. In geometry, what might you suggest as the analogue of strategy? In automated reasoning, for example, you have the resonance strategy to direct the reasoning; and to restrict it, you have the set of support strategy. (Of course, other effective strategies often come into play.) Without the use of strategy, I have observed that proving deep theorems and tackling difficult assignments other than proof finding are typically out of reach. Yes, even with today's extremely powerful computers, my position is that such power is far from enough. So, now, back to the question about geometry.
Typically, the geometer uses diagrams to help point the way (particularly for Tarskian geometry). In this column, the avoidance of such diagrams is key to the challenge I offer. Specifically, I shall ask you to prove a theorem that, mainly thanks to my colleague Michael Beeson, has been proved with the aid of an appropriate diagram and the use of OTTER. As you read this column, you may decide that I have an ulterior motive, in addition to the goal of stimulating further research. You might decide that I am curious about the power of programs other than Bill McCune's OTTER, clearly my favorite. You would be right.
The theorem in focus is called Satz 3.17 and, in clause form, is the following.
% following is Satz 3.17
-T(xa,xb,xc) | -T(xa1,xb1,xc) | -T(xa,xp,xa1) |
T(xp,f317(xa,xb,xc,xb1,xa1,xp),xc).
-T(xa,xb,xc) | -T(xa1,xb1,xc) | -T(xa,xp,xa1) |
T(xb,f317(xa,xb,xc,xb1,xa1,xp),xb1).
To attempt to prove this theorem, typically proved with an appropriate diagram, I offer you some Tarskian geometry axioms, followed by a number of theorems that might be of use; no diagram is offered. To be explicit, you are invited to use any automated reasoning you like, but you are not to use a diagram. Rather than focusing on the given challenge, you could, of course, begin by seeking a proof of the cited theorem, in part to initiate the formulation of an approach, possibly a new approach.
% Some Tarskian geometry axioms
E(x,y,y,x).
-E(x,y,z,v) | -E(x,y,z2,v2) | E(z,v,z2,v2).
-E(x,y,z,z) | x=y.
T(x,y,ext(x,y,w,v)).
E(y,ext(x,y,w,v),w,v).
-E(x,y,x1,y1) | -E(y,z,y1,z1) | -E(x,v,x1,v1) | -E(y,v,y1,v1) | -T(x,y,z)
| -T(x1,y1,z1) | x=y | E(z,v,z1,v1).
-T(x,y,x) | x=y.
-T(xa,xp,xc) | -T(xb,xq,xc) | T(xp,ip(xa,xp,xc,xb,xq),xb).
-T(xa,xp,xc) | -T(xb,xq,xc) | T(xq,ip(xa,xp,xc,xb,xq),xa).
-T(alpha,beta,gamma).
-T(beta,gamma,alpha).
-T(gamma,alpha,beta).
% Theorems and possible definitions
E(xa,xb,xa,xb).
-E(xa,xb,xc,xd) | E(xc,xd,xa,xb).
-E(xa,xb,xc,xd) | -E(xc,xd,xe,xf) | E(xa,xb,xe,xf).
-E(xa,xb,xc,xd) | E(xb,xa,xc,xd).
-E(xa,xb,xc,xd) | E(xa,xb,xd,xc).
E(xa,xa,xb,xb).
-T(xa,xb,xc) | -T(xa1,xb1,xc1) | -E(xa,xb,xa1,xb1) | -E(xb,xc,xb1,xc1)
| E(xa,xc,xa1,xc1).
xq = xa | -T(xq,xa,xd) | -E(xa,xd,xb,xc) | xd = ext(xq,xa,xb,xc).
-E(xb,xc,xa,xa) | xb=xc.
-E(xa,xb,xc,xd) | E(xb,xa,xd,xc).
-T(xa,xb,xc) | -T(xA,xB,xC) | -E(xa,xb,xB,xC)| -E(xb,xc,xA,xB)
| E(xa,xc,xA,xC).
T(xa,xb,xb).
-T(xa,xb,xc) | T(xc,xb,xa).
T(xa1,xa1,xb1).
-T(xa,xb,xc) | -T(xb,xa,xc) | xa = xb.
-T(xa,xb,xd) | -T(xb,xc,xd) | T(xa,xb,xc).
-T(xa,xb,xc) | -T(xa,xc,xd) | T(xb,xc,xd).
-T(xa,xb,xc) | -T(xb,xc,xd) | xb = xc | T(xa,xc,xd).
-T(xa,xb,xd) | -T(xb,xc,xd) | T(xa,xc,xd).
-T(xa,xb,xc) | -T(xa,xc,xd) | T(xa,xb,xd).
-T(xa,xb,xc) | -T(xb,xc,xd) | xb = xc | T(xa,xb,xd).
alpha != beta.
beta != gamma.
alpha != gamma.
T(xa,xb,ext(xa,xb,alpha,gamma)).
xb != ext(xa,xb,alpha,gamma).
I conjecture that finding a proof for Satz 3.17 without the use of any diagram will prove challenging.
I would indeed enjoy reading such a proof, should you find one; and I would even more enjoy knowing what program you used and how you proceeded.
Results of CADE Trustee Elections
An election was held from 16 September to 23 October 2016 to fill four positions on the board of trustees of CADE Inc.
9 candidates were nominated (in alphabetic order): Jasmin Blanchette, Silvio Ghilardi, Marijn Heule, Laura Kovács, André Platzer, Philipp Rümmer, Renate Schmidt, Stephan Schulz, and Christoph Weidenbach.
Ballots were sent by electronic mail to all members of AAR on 16 September, for a total of 1139 ballots. 128 valid ballots were returned, which translates to a participation level of 11.2% (as compared to 11.0% in 2015, 10.0% in 2014, 11.8% in 2013, 13.0% in 2012, 16.2% in 2011, and 13.3% in 2010).
The counting of the votes according to the single transferable vote algorithm described in the CADE Bylaws is detailed near the end of this newsletter.
The four candidates elected are Jasmin Blanchette, Laura Kovács, Renate Schmidt, and Christoph Weidenbach.
After this election, the following people are serving on the board of trustees of CADE Inc.:
- Jasmin Blanchette (elected 2016)
- Laura Kovács (elected 2016)
- Renate Schmidt (elected 2016)
- Christoph Weidenbach (elected 2016)
- Leonardo de Moura (CADE-26 program chair)
- Aart Middeldorp (elected 2015)
- Christoph Benzmüller (vice-president, elected 2015)
- Geoff Sutcliffe (re-elected 2014)
- Pascal Fontaine (elected 2014)
- Jürgen Giesl (elected 2014)
- Martin Giese (secretary)
- Neil Murray (treasurer)
On
behalf of the AAR and CADE Inc., I thank Peter Baumgartner, Maria Paola
Bonacina, Larry Paulson, and Brigitte Pientka for their service on the
board of trustees for the last three, resp. six years.
In particular, we thank Maria Paola Bonacina for her outstanding service
as President of CADE since 2013. In addition to the usual tasks of a
CADE president, she has untiringly guided the difficult processes leading
to the institution of both the CADE Best Paper Award and the Skolem Award.
We also thank Ashish Tiwari for his service as ex officio trustee for
IJCAR 2016.
I would also like to thank the remaining candidates, Silvio Ghilardi,
Marijn Heule, André Platzer, Philipp Rümmer, and Stephan Schulz for
running in the election.
Congratulations to Jasmin Blanchette, Laura Kovács, Renate Schmidt, and Christoph Weidenbach on being elected!
Christoph Weidenbach follows Maria Paola Bonacina as President of CADE
Maria Paola Bonacina's term as CADE trustee expired after the trustee elections 2016, and therefore also her office as president ended. The new Board of Trustees has elected Christoph Weidenbach as new president of CADE.
On the behalf of CADE and AAR, I congratulate Christoph Weidenbach on this honour and opportunity to serve CADE and the field of automated reasoning.
Also on behalf of the AAR and CADE, I would once more like to thank Maria Paola Bonacina for her outstanding effort and commitment as president of CADE during the past three years.
Search for New AAR Newsletter Editor
The Association for Automated Reasoning (AAR) is seeking a new AAR Newsletter Editor.
The AAR publishes an electronic newsletter, sent to all members, with a frequency of four times a year. The AAR newsletter is the major information channel for the automated reasoning community. Among other things, it can contain:
- announcements of relevant conferences, workshops, and summer schools,
- reports on such events,
- announcements of special issues of journals and magazines,
- brief technical articles,
- reports of experiments,
- open problems,
- presentations of systems,
- abstracts of theses,
- open letters, discussing issues of general interest in the AR community,
- announcements of job opportunities,
- CADE member information, e.g. concerning elections (as membership in CADE and AAR coincides).
Earlier issues of the AAR newsletter can be found at http://www.aarinc.org/Newsletters/.
The role of the newsletter editor is to collect and select information for inclusion in the newsletter, to solicit contributions, to technically edit the letter as a webpage, and to send out an announcement with link and summary. All this is done in close collaboration with the following people and roles:
- Larry Wos, President of AAR
- Martin Giese, Secretary of AAR and CADE
- Geoff Sutcliffe, AAR, CADE, and IJCAR webmaster
- Christoph Weidenbach, President of CADE, subcorporation of AAR
- Hans Jürgen Ohlbach, vice-president of AAR
- Christoph Benzmüller, CADE Representative on the AAR Board
- Pascal Fontaine, CADE Representative on the AAR Board
Acting as the AAR newsletter editor is an excellent opportunity for a deep and visible involvement in the AR community, as the role connects to all kinds of AR activities. The newsletter is a cornerstone for the community identity and development.
If you are interested in taking up this role, please reply to Martin Giese, secretary of AAR (secretary (at) aarinc (dot) org), until 15 December 2016. Please include (links to) information about your connection to automated reasoning. A decision will be taken by the boards of AAR and CADE.
Helmut Veith Stipend
Outstanding female students in the field of computer science who pursue (or plan to pursue) one of the master's programs in Computer Science at TU Wien taught in English are invited to apply for the Helmut Veith Stipend.
The stipend is dedicated to the memory of an outstanding computer scientist who worked in the fields of logic in computer science, computer-aided verification, software engineering, and computer security. Students who are awarded the Helmut Veith Stipend, which is co-funded by TU Wien, receive EUR 6000 annually for a duration of up to two years. In addition, all tuition fees are waived. Recipients of funding must demonstrate good progress during their studies and will have to reside in Austria during term time for the duration of their studies.
The application deadline is 30 November 2016. See the TU Wien's grants and scholarships web page for details.
The TPTP Needs Money
Maybe you have heard of the TPTP project, and maybe you are a user of the TPTP resources, either directly or indirectly. Direct uses include downloading the TPTP library, using the SystemOnTPTP interface, and being involved with CADE ATP System Competition (CASC). Indirect uses include using ATP systems whose development has benefited from direct use of the TPTP (Vampire, E, etc.), and using the Sledgehammer component of Isabelle (which calls the SystemOnTPTP service). If you appreciate what the TPTP does for automated reasoning, this message is for you.
Please consider making a donation of 100 units of a reasonable currency, to support the TPTP. A donation can be made as an unrestricted gift (tax deductable) to the University of Miami, explicitly to support the TPTP and related projects. Details of how to do this now, easily, and with my gratitude, are available on the TPTP web site.
Winter Schools
A One-Week Advanced School on Coq and Ssreflect:
Advance Software Verification and Computer Proof
The school will be in English and will target master students with already basic knowledge of Coq. The course will introduce formalization techniques based on the SSReflect proof language and the Mathematical Components library. See the school web site for details.
A One-Week Introductory Course:
Programming, Specifying, and Proving with the Coq System
This course is an introductory course intended for students in computer science who have very little knowledge of functional programming and no knowledge of computer proof. The background in mathematics will also be elementary.
At the end of the week, we expect that students will know how to write little programs (for instance number or list manipulations), write specifications about programs (for instance that a sorting algorithm does not loose data), and perform the proof that programs satisfy specifications. If you, one of your students, or one of your colleague wishes to learn about Coq from scratch, this may be the right event for you.
Registration is free but mandatory and every participant is responsible for their own accommodation, but we can provide some help finding affordable solutions. See the school web site for details.
Special Issue
AI Communications: Automated Reasoning
This special issue follows two successful 2016 events in Automated Reasoning: Artificial Intelligence and Theorem Proving (AITP 2016) and Practical Aspects of Automated Reasoning (PAAR 2016).
Important dates:
- Abstract submission: 8 January 2017
- Paper submission: 15 January 2017
- Notification of acceptance: 15 April 2017
- Final versions: 15 June 2017
The focus of the special issue will be on new combination of AI and Automated Reasoning, and on practical applications of Automated Reasoning.
The topics of interest include: Automated reasoning in propositional, first-order, higher-order and non-classical logics; AI and big-data methods in theorem proving and mathematics; Collaboration between automated and interactive theorem proving; Alignment and joint processing of formal, semi-formal, and informal libraries; Implementation of provers (SAT, SMT, resolution, tableau, instantiation- based, rewriting, logical frameworks, etc); Automated reasoning tools for all kinds of practical problems and applications; Methods for large-scale computer understanding of mathematics and science; Common-sense reasoning and reasoning in science; Combinations of linguistic/learning-based and semantic/reasoning methods; Pragmatics of automated reasoning within proof assistants; Practical experiences, usability aspects, feasibility studies; Evaluation of implementation techniques and automated reasoning tools; Performance aspects, benchmarking approaches; Non-standard approaches to automated reasoning, non-standard forms of automated reasoning, new applications; Implementation techniques, optimizations techniques, strategies and heuristics, fairness.
Participants of AITP 2016 and PAAR 2016, as well as other authors are invited to submit contributions.
This special issue welcomes original high-quality contributions that have been neither published in nor simultaneously submitted to other venues. Submissions will be peer-reviewed using the standard refereeing procedure of the AI Communications.
Full papers of a maximum extension of 15 pages should be prepared according to the AIComm style guidelines and submitted through the AIComm mstracker.
About PAAR: PAAR provides a forum for developers of automated reasoning tools to discuss and compare different implementation techniques, and for users to discuss and communicate their applications and requirements. PAAR brings together different groups to concentrate on practical aspects of the implementation and application of automated reasoning tools.
About AITP: Large-scale semantic processing and strong computer assistance of mathematics and science is our inevitable future. New combinations of AI and reasoning methods and tools deployed over large mathematical and scientific corpora will be instrumental to this task. AITP is the forum for discussing how to get there as soon as possible, and the force driving the progress towards that.
Conferences
MEMCODE 2016: Methods and Models for System Design, Call for Participation
MEMOCODE's objective is to emphasize the importance of models and methodologies in correct system design and development, and to bring together researchers and industry practitioners interested in all aspects of computer system development, to exchange ideas, research results and lessons learned. This covers all aspects of methods and models for system, hardware, and software design and development: formal foundations, engineering methods, tools, and experimental case studies.
Keynotes:
- André Platzer (Carnegie Mellon): How to Prove Hybrid Systems
- Robert de Simone (Inria): Multiform Logical Time for Me/Mo-codesign
- Sriram Rajamani (Microsoft Research): Trusted Cloud: How to make the cloud more secure
See the conference web site for details.
AITP 2017: Artificial Intelligence and Theorem Proving
Large-scale semantic processing and strong computer assistance of mathematics and science is our inevitable future. New combinations of AI and reasoning methods and tools deployed over large mathematical and scientific corpora will be instrumental to this task. The AITP conference is the forum for discussing how to get there as soon as possible, and the force driving the progress towards that.
Topics: AI and big-data methods in theorem proving and mathematics; Collaboration between automated and interactive theorem proving; Common-sense reasoning and reasoning in science; Alignment and joint processing of formal, semi-formal, and informal libraries; Methods for large-scale computer understanding of mathematics and science; Combinations of linguistic/learning-based and semantic/reasoning methods.
There will be several focused sessions on AI for ATP, ITP and mathematics, modern AI and big-data methods, and several sessions with contributed talks. The focused sessions will be based on invited talks and discussion oriented.
Confirmed participants/speakers:
- Cameron Freer, Gamalon Labs
- Georges Gonthier, INRIA Saclay
- Thomas C. Hales, University of Pittsburgh
- John Harrison, Intel
- Andreas Holmstrom
- Cezary Kaliszyk, University of Innsbruck
- Michael Kohlhase, FAU Erlangen-Nurnberg
- Tim Rocktäschel, University College London
- Stephan Schulz, DHBW Stuttgart
- Christian Szegedy, Google
- Josef Urban, Czech Technical University
- Robert Veroff, University of New Mexico
We solicit contributed talks. Selection of those will be based on extended abstracts/short papers of 2 pages formatted with easychair.cls. Submission is via EasyChair. The submission deadline is 1 December 2016. See the conference web site for details.
SCSS 2017: Symbolic Computation in Software Science
SCSS 2017 promotes research on theoretical and practical aspects of symbolic computation in software science. The symposium provides a forum for active dialog between researchers from several fields of computer algebra, algebraic geometry, algorithmic combinatorics, computational logic, and software analysis and verification.
SCSS 2017 solicits regular papers on all aspects of symbolic computation and their applications in software science. The topics of the symposium include, but are not limited to the following: automated reasoning; algorithm (program) synthesis and/or verification; formal methods for the analysis of network and system security; termination analysis and complexity analysis of algorithms (programs); extraction of specifications from algorithms (programs); related theorem proving methods and techniques; proof carrying code; generation of inductive assertion for algorithm (programs); algorithm (program) transformations; formalization and computerization of knowledge (maths, medicine, economy, etc.); component-based programming; computational origami; query languages (in particular for XML documents); and semantic web and cloud computing.
Invited speaker: Gérard Huet (Inria Paris, France).
Submissions of regular research papers are invited. There will be a Best Paper Award, sponsored by ATSN (the Tunisian Society for Digital Security). The proceedings of SCSS 2017 will be published in the EasyChair Proceedings in Computing (EPiC). After the symposium, we will have a special issue of the Journal of Symbolic Computation.
The abstract submission deadline is 20 November 2016. See the symposium web site for details.
LICS 2017: Logic in Computer Science
The LICS Symposium is an annual international forum on theoretical and practical topics in computer science that relate to logic, broadly construed. We invite submissions on topics that fit under that rubric.
Suggested, but not exclusive, topics of interest include: automata theory, automated deduction, categorical models and logics, concurrency and distributed computation, constraint programming, constructive mathematics, database theory, decision procedures, description logics, domain theory, finite model theory, formal aspects of program analysis, formal methods, foundations of computability, games and logic, higher-order logic, lambda and combinatory calculi, linear logic, logic in artificial intelligence, logic programming, logical aspects of bioinformatics, logical aspects of computational complexity, logical aspects of quantum computation, logical frameworks, logics of programs, modal and temporal logics, model checking, probabilistic systems, process calculi, programming language semantics, proof theory, real-time systems, reasoning about security and privacy, rewriting, type systems and type theory, and verification.
An award in honour of the late Stephen C. Kleene will be given for the best student paper(s), as judged by the program committee. The 2017 edition of the award is sponsored by the European Association for Theoretical Computer Science (EATCS). Full versions of up to three accepted papers, to be selected by the program committee, will be invited for submission to the Journal of the ACM. Additional selected papers will be invited to a special issue of Logical Methods in Computer Science.
Authors are required to submit a paper title and a short abstract by 3 January 2017 (firm). See the conference web site for details.
CAV 2017: Computer-Aided Verification
CAV 2017 is the 29th in a series dedicated to the advancement of the theory and practice of computer-aided formal analysis and synthesis methods for hardware and software systems. CAV considers it vital to continue spurring advances in hardware and software verification while expanding to domains such as cyber-physical, social, and biological systems. The conference covers the spectrum from theoretical results to concrete applications, with an emphasis on practical verification tools and the algorithms and techniques that are needed for their implementation. The proceedings of the conference will be published in the Springer LNCS series. A selection of papers will be invited to a special issue of Formal Methods in System Design and the Journal of the ACM.
Topics of interest include but are not limited to: Algorithms and tools for verifying models and implementations; Algorithms and tools for system synthesis; Mathematical and logical foundations of verification and synthesis; Specifications and correctness criteria for programs and systems; Deductive verification using proof assistants; Hardware verification techniques; Program analysis and software verification; Software synthesis; Hybrid systems and embedded systems verification; Compositional and abstraction-based techniques for verification; Probabilistic and statistical approaches to verification; Verification methods for parallel and concurrent systems; Testing and run-time analysis based on verification technology; Decision procedures and solvers for verification and synthesis; Applications and case studies in verification and synthesis; Verification in industrial practice; New application areas for algorithmic verification and synthesis; Formal models and methods for security; Formal models and methods for biological systems.
Submissions on a wide range of topics are sought, particularly ones that identify new research directions. CAV 2017 is not limited to topics discussed in previous instances of the conference. Authors concerned about the appropriateness of a topic may communicate with the conference chairs prior to submission.
Submissions will be in two categories: Regular Papers and Tool Papers. Papers must be submitted in PDF format by 24 January 2017. See the conference web site for details.
CADE-26: Conference on Automated Deduction
CADE is the major international forum at which research on all aspects of automated deduction is presented. High-quality submissions on the general topic of automated deduction, including foundations, applications, implementations, theoretical results, practical experiences and user studies are solicited.
- Logics of interest include propositional, first-order, equational, higher-order, classical, description, modal, temporal, many-valued, constructive, other non-classical, meta-logics, logical frameworks, type theory, set theory, as well as any combination thereof.
- Paradigms of interest include theorem proving, model building, constraint solving, computer algebra, model checking, proof checking, and their integration.
- Methods of interest include resolution, superposition, completion, saturation, term rewriting, decision procedures, model elimination, connection methods, tableaux, sequent calculi, natural deduction, as well as their supporting algorithms and data structures, including matching, unification, orderings, induction, indexing techniques, proof presentation and explanation, proof planning.
- Applications of interest include program analysis, verification and synthesis of software and hardware, formal methods, computational logic, computer mathematics, natural language processing, computational linguistics, knowledge representation, ontology reasoning, deductive databases, declarative programming, robotics, planning, and other areas of artificial intelligence.
Call for Papers
Submissions can be made in two categories: regular papers and system descriptions. The page limit in Springer LNCS style is 15 pages excluding references for regular papers and 10 pages excluding references for system descriptions. Submissions must be unpublished and not submitted for publication elsewhere. They will be judged on relevance, originality, significance, correctness, and readability. System descriptions must contain a link to a working system and will also be judged on usefulness and design. Proofs of theoretical results that do not fit in the page limit, executables of systems, and input data of experiments should be made available, via a reference to a website or in an appendix of the paper. For papers containing experimental evaluations, all data needed to rerun the experiments must be available. Reviewers will be encouraged to consider this additional material, but submissions must be self-contained within the respective page limit; considering the additional material should not be necessary to assess the merits of a submission. The review process will include a feedback/rebuttal period where authors will have the option to respond to reviewer comments. The PC chairs may solicit further reviews after the rebuttal period.
The proceedings of the conference will be published in the Springer LNCS/LNAI series. Formatting instructions and the LNCS style files are available from Springer.
At every CADE conference the Program Committee selects one of the accepted papers to receive the CADE Best Paper Award. The award recognizes a paper that the Program Committee collegially evaluates as the best in terms of originality and significance, having substantial confidence in its correctness. Overall technical quality, completeness, scholarly accuracy, and readability are also considered. Characteristics associated with a best paper include, for instance, introduction of a strong new technique or approach, solution of a long-standing open problem, introduction and solution of an interesting and important new problem, highly innovative application of known ideas or existing techniques, and presentation of a new system of outstanding power. Under exceptional circumstances, the Program Committee may give two awards (ex aequo) or give no award.
The abstract deadline is 11 February 2017. The full paper submission deadline is 18 February 2017. See the conference web site for details.
Call for Workshops, Tutorials, and System Competitions
Proposals for workshops, tutorials, and system competitions should be uploaded via EasyChair. The submission deadline is 5 December 2016.
Workshops
Workshop proposals for CADE-26 are solicited. The workshops will take place on 6 and 7 August 2017, before the main conference. Both well-established workshops and newer ones are encouraged. Similarly, proposals for workshops with a tight focus on a core automated reasoning specialization, as well as those with a broader, more applied focus, are very welcome.
Please provide the following information in your application document:
- Workshop title.
- Names and affiliations of organizers.
- Proposed workshop duration (from half a day to two days) and preferred day(s).
- Brief description of the goals and the scope of the workshop. Why is the workshop relevant for CADE?
- Is the workshop new or has it met previously? In the latter case information on previous meetings should be given (e.g., links to the program, number of submissions, number of participants).
- What are the plans for publication?
Tutorials
Tutorial proposals for CADE-26 are solicited. Tutorials are expected to be either half-day or full-day events, with a theoretical or applied focus, on a topic of interest for CADE-26. Proposals should provide the following information:
- Tutorial title.
- Names and affiliations of organizers.
- Proposed tutorial duration (from half a day to one days) and the preferred day.
- Brief description of the tutorial's goals and topics to be covered.
- Whether or not a version of the tutorial has been given previously.
System Competitions
The CADE ATP System Competition (CASC), which evaluates automated theorem proving systems for classical logics, has become an integral part of the CADE conferences.
Further system competition proposals are solicited. The goal is to foster the development of automated reasoning systems in all areas relevant for automated deduction in a broader sense. Proposals should include the following information:
- Competition title.
- Names and affiliations of organizers.
- Duration and schedule of the competition.
- Room/space requirements.
- Description of the competition task and the evaluation procedure.
- Is the competition new or has it been organized before? In the latter case information on previous competitions should be given.
- What computing resources are required and how will they be provided?
CSL 2017: Computer Science Logics
Computer Science Logic (CSL) is the annual conference of the European Association for Computer Science Logic (EACSL). It is an interdisciplinary conference, spanning across both basic and application oriented research in mathematical logic and computer science and is intended for computer scientists whose research involves logic, as well as for logicians working on issues essential for computer science.
CSL 2017 will be co-located with, and immediately preceded by, the Logic Colloquium 2017 (LC 2017). There will be a joint session of CSL 2017 and LC 2017 in the morning of August 20, as well as CSL-affiliated workshops during August 25-26.
Topics for CSL 2017 include (but are not limited to): automata and games, game semantics; automated deduction and interactive theorem proving; bounded arithmetic and propositional proof complexity; categorical logic and topological semantics; computational proof theory; constructive mathematics and type theory; decision procedures; domain theory; equational logic and rewriting; finite model theory; higher-order logic; lambda calculus and combinatory logic; linear logic and other substructural logics; logic programming and constraints; logical aspects of computational complexity; logical aspects of quantum computing; logic in database theory; logical foundations of programming paradigms; logical foundations of cryptography and information hiding; logics for multi-agent systems; modal and temporal logic; model checking and logic-based verification; nonmonotonic reasoning; SAT solving and automated induction; satisfiability modulo theories; specification, extraction and transformation of programs; and verification and program analysis.
Invited speakers:
- Phokion Kolaitis, University of California, Santa Cruz
- Wolfgang Thomas, RWTH Aachen
- Laura Kovács, Vienna University of Technology
- Stephan Kreutzer, Technische Universität Berlin
- Meena Mahajan, Institute of Mathematical Sciences, Chennai
- Marcus Veanes, Microsoft Research
The CSL 2017 conference proceedings will be published in Leibniz International Proceedings in Informatics (LIPIcs). Authors are invited to submit contributed papers of no more than 15 pages in LIPIcs style (including references), presenting not previously published work, fitting the scope of the conference. The abstract submission deadline is 24 March 2017. See the conference web site for details.
iFM 2017: Integrated Formal Methods, Call for Workshops
iFM 2017 is concerned with how the application of formal methods may involve modelling different aspects of a system which are best expressed using different formalisms. Correspondingly, different analysis techniques may be used to examine different system views, different kinds of properties, or simply in order to cope with the sheer complexity of the system. The iFM conference series seeks to further research into hybrid approaches to formal modelling and analysis; i.e., the combination of methods for system development, regarding modelling and analysis, and covering all aspects from language design through verification and analysis techniques to tools and their integration into software engineering practice.
Workshops can have the duration of one or two days. Prospective workshop organizers are requested to follow the guidelines below and are encouraged to contact the workshop chairs if any questions arise.
Workshop proposals must be written in English, not exceed 5 pages with a reasonable font and margins, and be submitted in PDF format via email to the iFM workshop chairs, Wolfgang Ahrendt and Michael Lienhardt.
Proposals should include:
- The name, the duration (1 or 2 days) and the preferred date of the proposed workshop
- A short description of the workshop.
- If applicable, a description of past versions of the workshop, including dates, organizers, submission and acceptance counts, and attendance.
- The publicity strategy that will be used by the workshop organizers to promote the workshop.
- The participant solicitation and selection process.
- The target audience and expected number of participants.
- Approximate budget proposal (see section Budget below for details).
- The equipment and any other resource necessary for the organization of the workshop.
- The name and short CV of the organizer(s).
- The publication plan (only invited speakers, no published proceedings, pre-/post-proceedings published with EPTCS/ENTCS/...).
The deadline for submission of workshop proposals is 19 December 2016. See the full call for workshops on the conference web site for details.
FroCoS 2017: Frontiers of Combining Systems
The 11th International Symposium on Frontiers of Combining Systems (FroCoS 2017) aims at disseminating and promoting progress in research areas related to the development of techniques for the integration, combination, and modularization of formal systems together with their analysis.
FroCoS 2017 will be co-located with the 26th International Conference on Automated Reasoning with Analytic Tableaux and Related Methods (TABLEAUX 2017) and the 8th International Conference on Interactive Theorem Proving (ITP 2017).
Typical topics of interest include (but are not limited to): combinations of logics (such as higher-order, first-order, temporal, modal, description or other non-classical logics); combination and integration methods in SAT and SMT solving; combination of decision procedures, satisfiability procedures, constraint solving techniques, or logical frameworks; combinations and modularity in ontologies; integration of equational and other theories into deductive systems; hybrid methods for deduction, resolution and constraint propagation; hybrid systems in knowledge representation and natural language semantics; combined logics for distributed and multi-agent systems; logical aspects of combining and modularizing programs and specifications; integration of data structures into constraint logic programming and deduction; combinations and modularity in term rewriting; applications of methods and techniques to the verification and analysis of information systems.
The proceedings of the symposium will be published in the Springer LNAI/LNCS series. The page limit in Springer LNCS style is 16 pages. The abstract submission deadline is 24 April 2017. See the conference web site for details.
ITP 2017: Interactive Theorem Proving
The ITP conference series is concerned with all topics related to interactive theorem proving, ranging from theoretical foundations to implementation aspects and applications in program verification, security, and formalization of mathematics. ITP is the evolution of the TPHOLs conference series to the broad field of interactive theorem proving. TPHOLs meetings took place every year from 1988 until 2009.
ITP welcomes submissions describing original research on all aspects of interactive theorem proving and its applications. Suggested topics include but are not limited to the following: formal aspects of hardware and software; formalizations of mathematics; improvements in theorem prover technology; user interfaces for interactive theorem provers; formalizations of computational models; verification of security algorithms; use of theorem provers in education; industrial applications of interactive theorem provers; concise and elegant worked examples of formalizations (proof pearls).
The proceedings of the symposium will be published in the Springer's LNCS series. All submissions must be original, unpublished, and not submitted concurrently for publication elsewhere. Furthermore, when appropriate, submissions are expected to be accompanied by verifiable evidence of a suitable implementation, such as the source files of a formalization for the proof assistant used. Submissions should be no more than 16 pages in length.
In addition to regular papers, described above, there will be a rough diamond section. Rough diamond submissions are limited to 6 pages and may consist of an extended abstract. They will be refereed and be expected to present innovative and promising ideas, possibly in an early form and without supporting evidence. Accepted diamonds will be published in the main proceedings and will be presented as short talks.
The abstract submission deadline is 3 April 2017. See the conference web site for details.
TABLEAUX 2017: Analytic Tableaux and Related Methods
TABLEAUX is the main international conference at which research on all aspects, theoretical foundations, implementation techniques, systems development and applications, of the mechanization of tableau-based reasoning and related methods is presented. TABLEAUX 2017 will be co-located with both the 11th International Symposium on Frontiers of Combining Systems (FroCoS 2017) and the 8th International Conference on Interactive Theorem Proving (ITP 2017).
Tableau methods offer a convenient and flexible set of tools for automated reasoning in classical logic, extensions of classical logic, and a large number of non-classical logics. For large groups of logics, tableau methods can be generated automatically. Areas of application include verification of software and computer systems, deductive databases, knowledge representation and its required inference engines, teaching, and system diagnosis.
Topics of interest include but are not limited to:
- tableau methods for classical and non-classical logics and their proof-theoretic foundations;
- related methods (SMT, model elimination, model checking, connection methods, resolution, BDDs, translation approaches);
- sequent calculi and natural deduction calculi for classical and non-classical logics, as tools for proof search and proof representation;
- flexible, easily extendable, light weight methods for theorem proving;
- novel types of calculi for theorem proving and verification in classical and non-classical logics;
- systems, tools, implementations, empirical evaluations and applications;
- implementation techniques;
- extensions of tableau procedures with conflict-driven learning, generation of proofs; compact (or human readable) representation of proofs;
- decision procedures, theoretically optimal procedures;
- applications of automated deduction to mathematics, software development, verification, deductive and temporal databases, knowledge representation, ontologies, fault diagnosis or teaching.
The conference proceedings will published in the Springer LNAI/LNCS series. Submissions are invited in two categories: research papers, which describe original theoretical research, original algorithms, or applications, with length up to 15 pages; system descriptions, with length up to 9 pages.
The TABLEAUX 2017 Best Paper Award will be presented to the best submission nominated and chosen by the Program Committee among the accepted papers. The eligibility criteria will place emphasis on the originality and significance of the contribution, but readability and the overall technical quality, including correctness and completeness of results, will be also considered.
The abstract submission deadline is 18 April 2017. See the conference web site for details.
TABLEAUX / FroCoS / ITP 2017, Call for Workshops and Tutorials
Three of the main conferences on automated reasoning—TABLEAUX, FroCoS, and ITP—will be held in Brasília, Brazil, between 25 and 29 September 2017. Following the long tradition of those events, we invite researchers and practitioners to submit proposals for co-located workshops and in-depth tutorials on topics relating to automated theorem proving and its applications. Workshops/tutorials can target the automated reasoning community in general, focus on a particular theorem proving system, or highlight more specific issues or recent developments.
Co-located events will take place between 23 and 24/25 September and will be held on the same premises as the main conference. Conference facilities are offered free of charge to the organisers. Workshop/tutorial-only attendees will enjoy a significantly reduced registration fee.
Detailed organisational matters such as paper submission and review process, or publication of proceedings, are up to the organisers of individual workshops. All accepted workshops/tutorials will be expected to have their program ready by 18 August 2017.
Proposals for workshops/tutorials should contain at least the following pieces of information:
- name and contact details of the main organiser(s)
- (if applicable:) names of additional organisers
- title and organisational style of event (tutorial, public workshop, project workshop, etc.)
- preferred length of workshop (between half day and two days)
- estimated number of attendees
- short (up to one page) description of topic
- (if applicable:) pointers to previous editions of the workshop, or to similar events
Proposals are invited to be submitted by email to Cláudia Nalon, no later than 9 December 2016. Selected events will be notified by 23 December 2016. The workshop/tutorial selection committee consists of the TABLEAUX, FroCoS, and ITP program chairs and the conference organisers.
Workshops
TTT: Type Theory Based Tools
TTT is a satellite workshop of POPL 2017. We have funding possibilities for students and young researchers, see below. Note the early deadline!
The aim of this workshop is to showcase modern tools based on type theory, whether designed for programming or for verification, whether academic projects or used in an industrial setting. It will provide a forum to highlight and discuss their common and their distinctive features, and the future directions of development of the tools. The program will consist of invited and contributed talks, and will encourage informal discussion. Abstracts will be displayed on the website of the workshop but there will be no proceedings. We solicit abstract submissions proposing demos, case studies, describing the impact of a theoretical result on practice, or any other aspect of the development and use of tools based on type theory. In particular, we welcome submissions about prototype implementations and promising work in progress, as soon as they have the potential of raising interesting discussions.
This workshop is funded by the EUTypes COST project. The program will include a plenary discussion on the role of the EUTypes project in the community and planning of activities for 2017.
Confirmed invited speakers:
- Robbert Krebbers, Delft University of Technology, Netherlands
- Aaron Tomb, Galois, US
Registration information will be soon available at the main POPL 2017 website.
The EUTypes COST project can fund students and young researchers from countries participating in the project to attend the workshop – check http://www.cost.eu/COST_Actions/ca/CA15123?parties to see if your country is listed. The application should include the following information:
- Your name
- Your institution
- The name of your supervisor(s)
- The URL of your webpage if you have one
- Your research topics or interests in 1 paragraph
For any query about this workshop, please contact the organizers.
Submissions for talks and demonstrations should be described in an extended abstract, between 1 and 2 pages in length. We suggest formatting the text using the two-column SIGPLAN LaTeX style (9pt font). Submissions are via EasyChair. The deadline is 30 November 2016.
MARS 2017: Models for Formal Analysis of Real Systems
The process of developing a detailed and accurate model usually takes a large amount of time, often months or years; without even starting a formal analysis. When publishing the results on a formal analysis in a scientific paper, details of the model have to be skipped due to lack of space, and often the lessons learnt from modelling are not discussed since they are not the main focus of the paper.
The workshop, affiliated with ETAPS 2017, aims at discussing exactly these unmentioned lessons. Examples are:
- Which formalism is chosen, and why?
- Which abstractions have to be made and why?
- How are important characteristics of the system modelled?
- Were there any complications while modelling the system?
- Which measures were taken to guarantee the accuracy of the model?
The workshop emphasises modelling over verification. In particular, we invite papers that present full Models of Real Systems, which may lay the basis for future formal analysis. The workshop will bring together researchers from different communities that all aim at verifying real systems and are developing formal models for such systems. Areas where large models often occur are within networks, (trustworthy) systems and software verification (from byte code up to programming- and specification languages). An aim of the workshop is to present different modelling approaches and discuss pros and cons for each of them.
Submissions must be unpublished and not be submitted for publication elsewhere. Contributions are limited to 8 pages EPTCS style (not counting the appendices), but shorter extended abstracts are welcome. The proceedings will be published as part of the open access series Electronic Proceedings in Theoretical Computer Science (EPTCS). The submission deadline is 13 January 2017. See the workshop web site for details.
DL 2017: Description Logics
The DL workshop is the major annual event of the description logic research community. It is the forum at which those interested in description logics, both from academia and industry, meet to discuss ideas, share information and compare experiences.
Invited speakers:
- Markus Krötzsch, Technical University of Dresden
- Andreas Pieris, University of Edinburgh
- Uli Sattler, University of Manchester
We invite contributions on all aspects of description logics, including but not limited to: foundations of description logics; extensions of description logics; integration of description logics with other formalisms; applications and use areas of description logics; and systems and tools around description logics.
Submissions may be of two types. Papers accepted at some conference can be submitted as accepted elsewhere together with a 1-page abstract that also specifies where the paper has been accepted. Other submissions consist of 11 pages LNCS plus references. There is no page limit on the list of references. If the paper should not appear in the proceedings, an additional 1-page abstract has to be submitted. The abstract submission deadline is 28 April 2017 (firm). See the workshop web site for details.
Book
Temporal Logics in Computer Science
This comprehensive text provides a modern and technically precise exposition of the fundamental theory and applications of temporal logics in computer science.
Part I presents the basics of discrete transition systems, including constructions and behavioural equivalences. Part II examines the most important temporal logics for transition systems. Part III studies their expressiveness and complexity. Part IV describes the main computational methods and decision procedures for model checking and model building based on tableaux, automata and games. Further information can be found on the Cambridge University Press web site.
Open Positions
Galois is Hiring in Oregon and Virginia, USA
Galois is looking for researchers, principal investigators, software engineers, and project leads, including those with expertise in functional programming, formal methods, machine learning, embedded systems, computer security, or networking.
We currently have a few Coq experts on staff, and a number of projects that use Coq or Lean including our project to formally verify Guardtime, Bluespec verification using Chlipala et al.'s Kami, and projects from Free & Fair, our elections spin out. For the exact available positions, please have a look at our web-site.
We have two offices: one in Portland, OR, and one in Arlington, VA. There are positions available at both locations. If you are interested, please send us your resume through the web site. Joey Dodds is also happy to answer any questions you might have.
Several Positions on Secure Compilation at Inria Paris, France
SECOMP is a research project aimed at building the first efficient formally secure compilers for realistic programming languages. The project brings together a core team at Inria Paris lead by Cătălin Hriţcu and external collaborators at University of Pennsylvania, Portland State University, MIT, Northeastern University, Microsoft Research, and Draper Labs. The core team at Inria Paris is generously funded for 5 years (roughly between 2017 and 2021) by a recently awarded ERC Starting Grant.
Over the duration of the project we are looking for excellent students and young researchers for Research Internship, PhD Student, PostDoc, Starting Researcher, and Research Engineer positions at Inria Paris. We can additionally support exceptional candidates for permanent Researcher positions funded and awarded competitively by Inria. More details about each of these positions are available online. Finally, we also have funding for sabbaticals and short-term visits to Paris for researchers with an interest in secure compilation. Please contact Cătălin Hriţcu for details.
Several Positions on Higher-Order Proof Automation at VU Amsterdam, the Netherlands, and Inria Nancy, France
Matryoshka is an ambitious research project that aims at developing efficient higher-order superposition provers and higher-order SMT (satisfiability modulo theories) solvers and integrating them in proof assistants. The project is funded by a European Research Council Starting Grant from March 2017 to February 2022. It is co-located between Vrije Universiteit Amsterdam (Jasmin Blanchette) in the Netherlands and Inria Nancy – Grand Est (Pascal Fontaine) in France.
Proof assistants are increasingly used to verify hardware and software and to formalize mathematics. However, despite the success stories, they remain very laborious to use. To make interactive verification more cost-effective, we propose to deliver powerful automation to users of proof assistants by fusing and extending two lines of research: automatic and interactive theorem proving. Our approach will be to enrich the superposition calculus and SMT with higher-order reasoning in a careful manner, to preserve their desirable properties. We will develop highly automatic provers building on modern superposition provers and SMT solvers, following a Russian doll architecture. To reach end users, these new provers will be integrated in proof assistants, including Coq, Isabelle/HOL, and the TLA+ Proof System.
We are looking for outstanding candidates for several Ph.D., postdoctoral, software engineer, and intern positions due to start in the next two years. Candidates should ideally have some experience with automatic or interactive theorem proving and be at ease with both theory and engineering. Please contact Jasmin Blanchette and Pascal Fontaine for more information.
Postdoc Position in Verification of Infinite-State Systems at the University of Iowa, USA
Project Supervisor:
Professor Cesare Tinelli, Computational Logic Center
Department of Computer Science, The University of Iowa
The project's overall objective is to develop and implement improved SMT-based verification/model checking techniques to verify safety properties of synchronous data-flow models of infinite-state embedded reactive software. The project will focus on contract-based compositional reasoning, automatic invariant discovery, static analysis of contracts, and interactive contract generation. The new techniques will be implemented in the Kind 2 model checker.
The ideal candidate would be one with:
- A PhD in Computer Science or a closely related field
- A strong background in logic and/or automated reasoning
- Knowledge of and experience with SAT/SMT and model checking
- Experience designing, building, and maintaining large software systems
- Excellent programming skills
- Solid programming experience in OCaml or similar languages
- Good English writing and speaking skills
- The ability to work in a collaborative environment
- A strong commitment to research excellence
The position is a full time appointment in the Computational Logic Center, with a starting salary of $58,000/year plus benefits which include health insurance, paid leave, and access to university facilities and activities. It will start on 1 January 2017 and is expected to have a duration of up to two years, based on performance and continued availability of funds. The position will remain open until filled.
Depending on the candidate's interests, there might be an opportunity to teach one course per year in the Computer Science department as a visiting assistant professor. This is, however, a separate position that would entail a corresponding reduction of effort in the postdoc appointment. It should be understood as an opportunity, not as a requirement for the postdoc contract.
Inquiries and applications should be sent via e-mail to to Prof. Tinelli with "Model Checking postdoc" in the subject. When sending an application please include your CV together with a brief description of your research accomplishments and interests, and the names of three references. See Prof. Tinelli's web site for more information.
Postdoc Position in Interactive Theorem Proving at Inria Sophia Antipolis, France
A postdoctoral position is available within the Marelle Inria team in Sophia Antipolis (south of France). The position is funded by the ANR Fastrelax research project on "Fast and reliable approximation" for numerical computation.
We are looking for a candidate who is interested in applying theorem proving techniques to effective numerical computation. One of our interests is to formalise bounds on polynomial approximations of functions (Berstein polynomials and Taylor models). Another interest is to formalize in Coq some results in real and complex analysis (differential equations, Padé approximants, generalized Fourier series or Lyapunov certificates).
Funding starts in 2017 and is available for 12 months. The net salary is around 2100 euros/month (including health insurance and social coverage). The candidate must have a PhD, and a strong knowledge in theorem proving and/or mathematics. Potential candidates can contact Laurent Théry or Laurence Rideau.
Ph.D. Position in Formal Methods for Information Security at ETH Zürich, Switzerland
The Information Security Group at ETH Zürich, headed by Prof. David Basin, carries out research on methods and tools for the analysis and construction of safe and secure systems. This includes methods for specifying systems, developing systems in correctness-preserving ways, and verifying or testing existing systems and infrastructures. Our goal is not only to build and analyze novel systems and security solutions, but also to develop better methods and tools for system engineering and quality assurance activities.
We have an open Ph.D. research position on "Formal Methods for Federated Identity Management". We seek to hire a researcher who will carry out research on the formal analysis of federated identity management systems, like SAML and OAuth 2.0. The project's main objectives are to distill requirements and designs for "next generation federated identity management" and to bring current verification tools, in particular our Tamarin prover, up to the level where such protocols can be automatically analyzed on a realistic scale with respect to both security and privacy properties.
The project, which will be carried out together with partners at Zurich Kantonal Bank (ZKB), will run for approximately 3 years and provide the possibility of carrying out a Ph.D. during this period. As part of this project, the researcher will spend time with ZKB learning about the systems under consideration and state-of-the-art approaches to their design and analysis.
The ideal candidate for this position is an enthusiastic, outstanding researcher with a strong background and interest in one or more of the following areas: formal methods or mathematical logic; information security or cryptography; automated security protocol verification tools. Candidates with a strong theoretical background in related areas are also encouraged to apply. ETH Zürich regulations require Ph.D. candidates to hold a Master's or equivalent degree (e.g. Diplom). The project, which is funded by the Zurich Information Security Center, and will be supervised by Prof. David Basin together with Dr. Ralf Sasse.
ETH Zürich regulations require doctoral students to hold a Master's or equivalent degree (e.g. Diplom). Applications should include a curriculum vitae, a brief description of research interests, transcripts of grades, 2-3 letters of recommendation from teachers or employers, and, if possible, the Master's or Bachelor's thesis and publications. Applications and informal inquiries should be sent to Ralf Sasse.
Research Internships in Program Analysis at Google in California and New York, USA
Google has a number of research internship openings in program analysis for 2017. Possible topics include the following: Identification of vulnerabilities in Android apps through static analysis; Distributed static analysis of large applications; Dynamic symbolic execution; Automated test case generation.
Internships could start as early as January 2017 and as late as September 2017, and typically last 14 weeks, but extensions are possible. Positions are available in Mountain View, CA and New York, NY.
Ideal candidates would have strong research background and solid (C++) programming skills. Please send CVs and referrals to Domagoj Babic.
Counting of the Ballots of the CADE Trustee Elections
An election was held to fill 4 positions. Jasmin Blanchette, Silvio Ghilardi, Marijn Heule, Laura Kovács, André Platzer, Philipp Rümmer, Renate Schmidt, Stephan Schulz, and Christoph Weidenbach were nominated. 128 valid ballots were returned. Therefore, in each iteration of the single transferable vote algorithm described in the CADE Bylaws, a candidate is elected if she or he gets at least 65 first preference votes. Otherwise, the votes of the candidate with the least first preference votes are redistributed.
The following table reports the initial distribution of preferences among the candidates:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | 4th pref. | 5th pref. | 6th pref. | 7th pref. | 8th pref. | 9th pref. | no supp. |
| Jasmin Blanchette | 46 | 31 | 16 | 9 | 6 | 2 | 6 | 3 | 1 | 8 |
| Silvio Ghilardi | 6 | 6 | 7 | 4 | 9 | 8 | 7 | 10 | 28 | 43 |
| Marijn Heule | 5 | 10 | 11 | 14 | 9 | 12 | 13 | 17 | 6 | 31 |
| Laura Kovács | 9 | 20 | 13 | 16 | 17 | 11 | 10 | 5 | 2 | 25 |
| André Platzer | 6 | 10 | 10 | 7 | 11 | 11 | 16 | 16 | 11 | 30 |
| Philipp Rümmer | 9 | 10 | 13 | 16 | 20 | 17 | 10 | 9 | 7 | 17 |
| Renate Schmidt | 15 | 14 | 18 | 22 | 12 | 10 | 7 | 3 | 4 | 23 |
| Stephan Schulz | 17 | 7 | 15 | 17 | 14 | 11 | 10 | 9 | 6 | 22 |
| Christoph Weidenbach | 15 | 18 | 20 | 16 | 9 | 13 | 9 | 7 | 4 | 17 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of Marijn Heule, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | 4th pref. | 5th pref. | 6th pref. | 7th pref. | 8th pref. | no supp. |
| Jasmin Blanchette | 47 | 32 | 18 | 9 | 3 | 4 | 6 | 1 | 8 |
| Silvio Ghilardi | 6 | 7 | 6 | 6 | 8 | 10 | 12 | 30 | 43 |
| Laura Kovács | 12 | 18 | 16 | 21 | 13 | 13 | 7 | 3 | 25 |
| André Platzer | 6 | 11 | 11 | 8 | 13 | 16 | 21 | 12 | 30 |
| Philipp Rümmer | 9 | 12 | 20 | 13 | 23 | 14 | 11 | 9 | 17 |
| Renate Schmidt | 15 | 15 | 19 | 23 | 14 | 12 | 3 | 4 | 23 |
| Stephan Schulz | 17 | 10 | 13 | 20 | 16 | 10 | 13 | 7 | 22 |
| Christoph Weidenbach | 16 | 21 | 20 | 13 | 13 | 14 | 10 | 4 | 17 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of Silvio Ghilardi, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | 4th pref. | 5th pref. | 6th pref. | 7th pref. | no supp. |
| Jasmin Blanchette | 47 | 33 | 19 | 9 | 3 | 5 | 4 | 8 |
| Laura Kovács | 12 | 21 | 18 | 17 | 19 | 9 | 7 | 25 |
| André Platzer | 7 | 11 | 12 | 11 | 11 | 23 | 23 | 30 |
| Philipp Rümmer | 9 | 13 | 21 | 18 | 18 | 18 | 14 | 17 |
| Renate Schmidt | 17 | 15 | 19 | 22 | 17 | 9 | 6 | 23 |
| Stephan Schulz | 18 | 12 | 12 | 21 | 16 | 12 | 15 | 22 |
| Christoph Weidenbach | 18 | 20 | 21 | 11 | 16 | 14 | 11 | 17 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of André Platzer, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | 4th pref. | 5th pref. | 6th pref. | no supp. |
| Jasmin Blanchette | 47 | 40 | 15 | 8 | 5 | 5 | 8 |
| Laura Kovács | 13 | 21 | 22 | 17 | 19 | 11 | 25 |
| Philipp Rümmer | 10 | 13 | 25 | 24 | 19 | 20 | 17 |
| Renate Schmidt | 20 | 16 | 24 | 20 | 15 | 10 | 23 |
| Stephan Schulz | 19 | 13 | 13 | 25 | 15 | 21 | 22 |
| Christoph Weidenbach | 19 | 22 | 21 | 11 | 21 | 17 | 17 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of Philipp Rümmer, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | 4th pref. | 5th pref. | no supp. |
| Jasmin Blanchette | 52 | 40 | 14 | 7 | 7 | 8 |
| Laura Kovács | 15 | 24 | 23 | 24 | 17 | 25 |
| Renate Schmidt | 22 | 19 | 29 | 22 | 13 | 23 |
| Stephan Schulz | 19 | 15 | 24 | 25 | 23 | 22 |
| Christoph Weidenbach | 20 | 27 | 20 | 18 | 26 | 17 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of Laura Kovács, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | 4th pref. | no supp. |
| Jasmin Blanchette | 58 | 42 | 9 | 11 | 8 |
| Renate Schmidt | 26 | 26 | 35 | 18 | 23 |
| Stephan Schulz | 20 | 22 | 35 | 29 | 22 |
| Christoph Weidenbach | 23 | 31 | 25 | 32 | 17 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of Stephan Schulz, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | no supp. |
| Jasmin Blanchette | 72 | 36 | 12 | 8 |
| Renate Schmidt | 29 | 39 | 37 | 23 |
| Christoph Weidenbach | 25 | 43 | 43 | 17 |
Now, Jasmin Blanchette reaches at least 65 first preference votes, and is elected.
To find the next elected candidate, we redistribute the votes of Jasmin Blanchette and get the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | 4th pref. | 5th pref. | 6th pref. | 7th pref. | 8th pref. | no supp. |
| Silvio Ghilardi | 8 | 8 | 7 | 7 | 9 | 8 | 10 | 28 | 43 |
| Marijn Heule | 9 | 15 | 11 | 13 | 12 | 13 | 18 | 6 | 31 |
| Laura Kovács | 20 | 21 | 14 | 18 | 11 | 11 | 6 | 2 | 25 |
| André Platzer | 10 | 14 | 8 | 9 | 13 | 17 | 15 | 12 | 30 |
| Philipp Rümmer | 16 | 12 | 17 | 22 | 15 | 13 | 9 | 7 | 17 |
| Renate Schmidt | 21 | 21 | 23 | 15 | 11 | 7 | 3 | 4 | 23 |
| Stephan Schulz | 20 | 12 | 20 | 15 | 13 | 10 | 10 | 6 | 22 |
| Christoph Weidenbach | 24 | 22 | 21 | 10 | 13 | 9 | 8 | 4 | 17 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of Silvio Ghilardi, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | 4th pref. | 5th pref. | 6th pref. | 7th pref. | no supp. |
| Marijn Heule | 11 | 15 | 13 | 17 | 10 | 12 | 19 | 31 |
| Laura Kovács | 21 | 22 | 16 | 17 | 14 | 9 | 4 | 25 |
| André Platzer | 11 | 15 | 8 | 11 | 15 | 18 | 20 | 30 |
| Philipp Rümmer | 16 | 14 | 18 | 23 | 15 | 16 | 9 | 17 |
| Renate Schmidt | 23 | 21 | 24 | 14 | 11 | 6 | 6 | 23 |
| Stephan Schulz | 20 | 16 | 18 | 15 | 15 | 12 | 10 | 22 |
| Christoph Weidenbach | 26 | 21 | 22 | 9 | 13 | 12 | 8 | 17 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of André Platzer, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | 4th pref. | 5th pref. | 6th pref. | no supp. |
| Marijn Heule | 11 | 16 | 19 | 13 | 13 | 25 | 31 |
| Laura Kovács | 23 | 23 | 16 | 20 | 14 | 7 | 25 |
| Philipp Rümmer | 18 | 13 | 27 | 23 | 17 | 13 | 17 |
| Renate Schmidt | 27 | 27 | 19 | 13 | 12 | 7 | 23 |
| Stephan Schulz | 22 | 17 | 18 | 18 | 19 | 12 | 22 |
| Christoph Weidenbach | 27 | 26 | 17 | 14 | 14 | 13 | 17 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of Marijn Heule, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | 4th pref. | 5th pref. | no supp. |
| Laura Kovács | 27 | 25 | 20 | 18 | 13 | 25 |
| Philipp Rümmer | 18 | 26 | 25 | 21 | 21 | 17 |
| Renate Schmidt | 28 | 27 | 25 | 15 | 10 | 23 |
| Stephan Schulz | 25 | 15 | 24 | 21 | 21 | 22 |
| Christoph Weidenbach | 30 | 29 | 13 | 20 | 19 | 17 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of Philipp Rümmer, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | 4th pref. | no supp. |
| Laura Kovács | 33 | 26 | 24 | 20 | 25 |
| Renate Schmidt | 33 | 34 | 25 | 13 | 23 |
| Stephan Schulz | 25 | 26 | 30 | 25 | 22 |
| Christoph Weidenbach | 37 | 26 | 20 | 28 | 17 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of Stephan Schulz, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | no supp. |
| Laura Kovács | 38 | 38 | 27 | 25 |
| Renate Schmidt | 43 | 38 | 24 | 23 |
| Christoph Weidenbach | 45 | 30 | 36 | 17 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of Laura Kovács, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | no supp. |
| Renate Schmidt | 64 | 41 | 23 |
| Christoph Weidenbach | 57 | 54 | 17 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of Christoph Weidenbach, one gets the following table:
| Candidate | 1st pref. | no supp. |
| Renate Schmidt | 105 | 23 |
Now, Renate Schmidt reaches at least 65 first preference votes, and is elected.
To find the next elected candidate, we redistribute the votes of Renate Schmidt and get the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | 4th pref. | 5th pref. | 6th pref. | 7th pref. | no supp. |
| Silvio Ghilardi | 11 | 8 | 9 | 11 | 8 | 9 | 29 | 43 |
| Marijn Heule | 10 | 20 | 12 | 16 | 15 | 18 | 6 | 31 |
| Laura Kovács | 24 | 24 | 18 | 15 | 13 | 7 | 2 | 25 |
| André Platzer | 13 | 12 | 12 | 12 | 21 | 14 | 14 | 30 |
| Philipp Rümmer | 18 | 14 | 28 | 18 | 15 | 10 | 8 | 17 |
| Stephan Schulz | 23 | 20 | 20 | 15 | 10 | 12 | 6 | 22 |
| Christoph Weidenbach | 29 | 25 | 22 | 13 | 9 | 9 | 4 | 17 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of Marijn Heule, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | 4th pref. | 5th pref. | 6th pref. | no supp. |
| Silvio Ghilardi | 12 | 7 | 11 | 13 | 11 | 31 | 43 |
| Laura Kovács | 27 | 28 | 20 | 14 | 11 | 3 | 25 |
| André Platzer | 14 | 13 | 12 | 25 | 19 | 15 | 30 |
| Philipp Rümmer | 18 | 25 | 27 | 17 | 14 | 10 | 17 |
| Stephan Schulz | 26 | 19 | 24 | 14 | 16 | 7 | 22 |
| Christoph Weidenbach | 31 | 31 | 18 | 14 | 13 | 4 | 17 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of Silvio Ghilardi, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | 4th pref. | 5th pref. | no supp. |
| Laura Kovács | 30 | 29 | 22 | 14 | 8 | 25 |
| André Platzer | 15 | 15 | 17 | 24 | 27 | 30 |
| Philipp Rümmer | 18 | 31 | 26 | 18 | 18 | 17 |
| Stephan Schulz | 29 | 19 | 25 | 17 | 16 | 22 |
| Christoph Weidenbach | 35 | 28 | 18 | 18 | 12 | 17 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of André Platzer, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | 4th pref. | no supp. |
| Laura Kovács | 36 | 27 | 24 | 16 | 25 |
| Philipp Rümmer | 21 | 41 | 23 | 26 | 17 |
| Stephan Schulz | 32 | 21 | 30 | 23 | 22 |
| Christoph Weidenbach | 38 | 30 | 22 | 21 | 17 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of Philipp Rümmer, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | no supp. |
| Laura Kovács | 44 | 32 | 27 | 25 |
| Stephan Schulz | 36 | 39 | 31 | 22 |
| Christoph Weidenbach | 47 | 32 | 32 | 17 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of Stephan Schulz, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | no supp. |
| Laura Kovács | 59 | 44 | 25 |
| Christoph Weidenbach | 63 | 48 | 17 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of Laura Kovács, one gets the following table:
| Candidate | 1st pref. | no supp. |
| Christoph Weidenbach | 111 | 17 |
Now, Christoph Weidenbach reaches at least 65 first preference votes, and is elected.
To find the next elected candidate, we redistribute the votes of Christoph Weidenbach and get the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | 4th pref. | 5th pref. | 6th pref. | no supp. |
| Silvio Ghilardi | 16 | 7 | 13 | 10 | 10 | 29 | 43 |
| Marijn Heule | 18 | 16 | 18 | 18 | 21 | 6 | 31 |
| Laura Kovács | 29 | 27 | 22 | 14 | 8 | 3 | 25 |
| André Platzer | 13 | 18 | 15 | 20 | 18 | 14 | 30 |
| Philipp Rümmer | 23 | 27 | 22 | 17 | 12 | 10 | 17 |
| Stephan Schulz | 28 | 26 | 18 | 14 | 13 | 7 | 22 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of André Platzer, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | 4th pref. | 5th pref. | no supp. |
| Silvio Ghilardi | 17 | 9 | 16 | 10 | 33 | 43 |
| Marijn Heule | 19 | 18 | 24 | 26 | 10 | 31 |
| Laura Kovács | 35 | 25 | 24 | 13 | 6 | 25 |
| Philipp Rümmer | 25 | 38 | 18 | 18 | 12 | 17 |
| Stephan Schulz | 31 | 29 | 19 | 18 | 9 | 22 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of Silvio Ghilardi, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | 4th pref. | no supp. |
| Marijn Heule | 23 | 25 | 21 | 28 | 31 |
| Laura Kovács | 37 | 29 | 26 | 11 | 25 |
| Philipp Rümmer | 30 | 34 | 26 | 21 | 17 |
| Stephan Schulz | 36 | 26 | 25 | 19 | 22 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of Marijn Heule, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | 3rd pref. | no supp. |
| Laura Kovács | 44 | 39 | 20 | 25 |
| Philipp Rümmer | 42 | 35 | 34 | 17 |
| Stephan Schulz | 40 | 32 | 34 | 22 |
No candidate reaches at least 65 first preference votes.
By redistributing the votes of Stephan Schulz, one gets the following table:
| Candidate | 1st pref. | 2nd pref. | no supp. |
| Laura Kovács | 66 | 37 | 25 |
| Philipp Rümmer | 55 | 56 | 17 |
Now, Laura Kovács reaches at least 65 first preference votes, and is elected.
To summarize, the 4 candidates elected are Jasmin Blanchette, Renate Schmidt, Christoph Weidenbach, and Laura Kovács.
The Editor's Corner
This column is back, after a brief hiatus to avoid interfering with the CADE trustee election. I am very grateful for the support for my nomination and am looking forward to serve on the CADE board of trustees.
I would like to use this opportunity to thank Maria Paola Bonacina for her outstanding service as president of CADE and to congratulate Christoph Weidenbach on his election as the new CADE president. In her many years on the board of trustees, including the last three years as president, Maria Paola has done a lot for our community. Notably, she was one of the key people behind the IJCAR conglomerate and has played an important role in keeping it alive. She is also known for her very reasoned and insightful emails. Christoph also has a long history of service at CADE and beyond. In my collaborations with him, I have seen up close how much he cares about the future of automated deduction and of CADE.
As a result of the trustee election, we are looking for a new AAR newsletter editor. This is a nice duty that takes about half a day times four or five times a year. Go for it! For my part, I'll use the free time to do more research (just kidding).
* * *
I often like to emphasize the synergy between automatic theorem proving (ATP) and interactive theorem proving (ITP). Proof assistants not only incorporate proof procedures that emerged in the ATP world; they also integrate state-of-the-art ATP systems to discharge proof obligations automatically.
But there's another way to combine ATP and ITP, which can be quite appealing to ITP-minded researchers in search of an excuse to attend CADE and IJCAR. Namely: Automated deduction has a rich metatheory, which deserves to be formalized in a proof assistant. In our IJCAR 2016 paper, Mathias Fleury, Christoph Weidenbach, and I wrote:
Researchers in automated reasoning spend a significant portion of their work time specifying logical calculi and proving metatheorems about them. These proofs are typically carried out with pen and paper, which is error-prone and can be tedious. As proof assistants are becoming easier to use, it makes sense to employ them.
The objective of formalization work is not to eliminate paper proofs, but to complement them with rich formal companions. Formalizations help catch mistakes, whether superficial or deep, in specifications and theorems; they make it easy to experiment with changes or variants of concepts; and they help clarify concepts left vague on paper.
There have been many formalizations of inference systems in proof assistants, but often researchers were satisfied once they had established the completeness of some minimalistic version of first-order logic. The first formalization of Alan Robinson's first-order resolution calculus, from 1965, was presented over half a century later at ITP 2016 by Anders Schlichtkrull. The most impressive achievement in this area might well be Nicolas Peltier's formalization of superposition, which appeared in the Archive of Formal Proofs just two months ago.
My hope is that we will soon catch up with modern research in automated deduction. Once the basic libraries and methodology are in place, and assuming that local expertise is available, formalization becomes a more satisfying enterprise than writing (and modifying and checking) paper proofs.
Recently, I have been developing and formalizing a generalized version of Michel Ludwig and Uwe Waldmann's Transfinite Knuth–Bendix Order (TKBO). To test the Isabelle library of syntactic ordinals I am developing together with Dmitriy Traytel, I formalized a paper proof of one of the lemmas needed to show that TKBO is stable under substitution.
I spent an enjoyable evening (which ended at about 1:30 AM) formalizing Michel and Uwe's argument using the Isabelle syntactic ordinals. The result corresponds almost one-to-one to their impeccable proof. I had to define the concept of degree of an ordinal, and to prove a pair of decomposition lemmas to justify the first two reasoning steps, but once these concepts were in place, I could discharge all but one step automatically. The result (excluding the degree and decomposition lemmas) is shown below, next to the informal proof written by Uwe. (Click the images to enlarge them.)
With a detailed enough paper proof, formalization was easy and could be performed by a tired (but motivated) researcher. This convinced me once again that the main advantage of paper proofs is that they allow a sketchy, superficial style; but sketchy paper proofs are not reliable, as observed by Leslie Lamport (How to Write a Proof, Section 4.1). Uwe told me he and Michel spent considerably more time coming up with their detailed paper proof than I spent formalizing it.
Thus, the tedious step is usually not from a paper proof to a formal proof, but from a sketchy paper proof to a rigorous proof, regardless of whether the latter is checkable by a machine. To extremely detail-oriented people like Leslie or Uwe, the rigorous proof can be expressed on paper; but they are a minority, and most of us can certainly benefit from the support of a proof assistant, just like it would not cross our minds to develop programs on paper.
As a reviewer, I find typical ITP papers much easier to assess than CADE or IJCAR papers. When every statement is proved formally in a proof assistant, there is no need to study the proof closely. It suffices to check that the definitions of the symbols arising in the main theorems are reasonable (e.g., addition is really addition), that sanity checks have been performed on them (e.g., extra lemmas or tests), and that no new axioms are introduced without careful justification if at all. In contrast, a CADE paper, with its metatheoretical proofs, requires a much closer examination; the resulting review typically contains a hand-wavy statement to the effect that "the proofs look plausible." Checking informal proofs of the kinds that arise in computer science is an unsatisfying task, and I know very few people who are good at it. It is almost as unpleasant as modifying an existing LaTEX proof.
I am now convinced that the time is ripe for formal proofs of the metatheory at CADE and IJCAR. And I am not alone—Nicolas Peltier and Christoph Weidenbach also appear to share this belief, and probably many others. The learning curve of proof assistants is not easy (one user quipped that "there's no learning curve, it's a series of cliffs"), but once you get addicted there is no going back. The Coq and Agda proof assistants are very popular at the POPL and ICFP conferences, to formalize the metatheory of programming languages. What is stopping us from using proof assistants more systematically at CADE, FroCoS, IJCAR, LPAR, and TABLEAUX as well?